1. Home
2. Blog
3. Image conversion from cartesian to cylindrical coordinates

Image conversion from cartesian to cylindrical coordinates

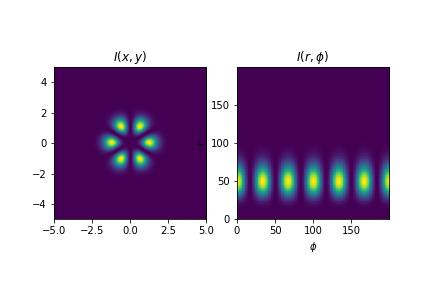
Introduction

Suppose that one has some picture of a cylindrical structure, as for example a Gaussian light beam or Laguerre-Gauss laser modes. How to convert the image from \(xy\) cartesian coordinates to \(r\theta\) cylindrical coordinates? This is particularly important if the pattern does not have azimuthal symmetry and rotates. How to determine the rotation angle?

Consider the light beam below, produced which can be understood as the interference between two LG modes. How to perform the coordinate transformation in a numerically efficient way using Python?

%pylab inline
xx = linspace(-5,5, 1000)
yy = linspace(-5,5, 1000)

x, y = meshgrid(xx,yy)
v = x + 1j * y
r = abs(v)
phi = angle(v)

offset = deg2rad(0)
m = 3
nbins = 200 # If this is too large, some distortion in the angle due to pixelation

profile =  r**m * cos(m*(theta+phi)) * exp(-r**2)

rr = linspace(0,5,nbins)
pphi = linspace(-pi,pi,nbins)
Phi, R = meshgrid(pphi, rr)
profile_r_phi = R**m * cos(m*(Phi+offset)) * exp(-R**2)

subplot(121)
title(r'$I(x,y)$')

dx = (xx[1]-xx[0])/2
dy = (yy[1]-yy[0])/2
extent_xy=[xx[0]-dx, xx[-1]+dx, yy[0]-dy, yy[-1]+dy]

imshow(absolute(profile)**2, origin='lower', extent=extent_xy)
subplot(122)
#im = imshow(angle(profile), cmap=cm.gray)
#colorbar(im)
title(r'$I(r,\phi)$')

imshow(absolute(profile_r_phi)**2, origin='lower')
xlabel("$\\phi$")
ylabel("r")

savefig(r"assets\xy_rphi_initialproblem.png")

Radial dependence

Suppose we want to find \(I(r)\). How do we do this, given that we know \(I(x,y)\)? We can build a map that indicates the coordinate of each pixel in the coordinate system of interest, as performed above for x,y,r,phi. We can use histograms to verify how frequent each value of r,phi appears in the image. Below we have the histogram of r in an array whose size is the same as profile. Notice that the growth is linear with r until the corners of the array are reached at \(r=5\). Resembles, at least slightly, the Jacobian of the coordinate transformation. Suppose now that the histogram of \(r\) is weighted by the intensity profile, could this be equivalent to the coordinate transformation?

h = histogram(r, bins=nbins, weights=absolute(profile)**2)
hx = h[1][:-1]
hy = h[0]

h2 = histogram(r, bins=nbins)

subplot(211)
title('num of array elems with given r values')
plot(hx, h2[0], 'k.')

# Notice that the frequency of r[i] is proportional to r. Jacobian?
# It is necessary to normalize by h2!

subplot(212)
title('intensity vs radius?')
plot(hx, hy, 'k.')

tight_layout()

savefig(r"assets\xy_rphi_radial_histogram.png")

It’s very close indeed, however it is necessary to normalize by the number of pixels whose radius is r. Below this correction is performed and the theory and numerical conversion are compared. Notice the perfect matching, which indicates the present procedure is adequate.

title('avg intensity vs radius')

h1 = histogram(r, bins=nbins, weights=absolute(profile)**2)
h2 = histogram(r, bins=nbins)

hx = h1[1][:-1]
hy = h1[0]/h2[0]

factor = 1 if m==0 else 2

plot(hx, hy, 'k.', label='histogram transformation')
plot(hx, hx**(2*m) * exp(-2*hx**2)/factor, label='theory')
legend(loc=0)
savefig(r"assets\xy_rphi_radial_histogram_2.png")

Angular dependence

To obtain the angular dependence is similar, however some extra care must be taken. Consider the histogram of phi, weighted by 1 or the intensity profiles. Notice that while the radial distortion is due to pixels close to the image borders, in the azimuthal direction there are more pixels along certain directions (diagonals). This is important to notice because the contribution due to some angles can be disproportionate. Also, close to \(r=0\), some angles may be unavailable due to pixelation.

h = histogram(phi, bins=nbins, weights=absolute(profile)**2)
hx = h[1][:-1]*180/pi
hy = h[0]

h2 = histogram(phi, bins=nbins)

subplot(211)
plot(hx, h2[0], 'k.')
# Notice the distortion at the most frequent phi values
# The most frequent phi values are at the diagonals

subplot(212)
title('intensity vs angle?')
plot(hx, hy, 'k.')

tight_layout()
savefig(r"assets\xy_rphi_angular_histogram.png")

If the histogram is normalized as before, there will be some distortion due to the diagonals. To avoid this, we filter the image radially and obtain the following result is obtained. Notice how the numerical transformation nicely matches the theoretically expected result.

title('intensity vs angle at given radius')

rad = sqrt(1+m)/2
width = 0.3 # If this is too large, some distortion appear due to the frame edges and pixelation
mask = 1.0 * (r> rad-width/2) * (r < rad+width/2)

h1 = histogram(phi, bins=nbins, weights=absolute(profile)**2 * mask)
h2 = histogram(phi, bins=nbins, weights=mask)
hx = h1[1][:-1]*180/pi
hy = h1[0]/h2[0]

plot(hx, hy, 'k.', label='Numerical transformation')

ampl = rad**(2*m) * exp(-2*rad**2)
plot(hx, ampl*cos(m * (pi*hx/180 + offset))**2, label='Theory')

legend(loc=0)
savefig(r"assets\xy_rphi_angular_histogram_2.png")

Radial and angular dependence

Since the above considerations allowed to obtain the intensity vs radius or intensity vs angle, would it be possible to obtain intensity as a function of radius and angle? We can use 2d histograms to obtain this transformation, analogously to the previous cases. Some distinctions are important here. histogram2d() does not accept r, phi and profile as 2d arrays, such ravel() is used to convert these matrices to 1D ndarrays. Also, close to r=0 there will be several angles which cannot be found, such the normalization will be undefined. In such cases it could be possible to interpolate the data between well defined values. Notice that this is not a limitation of the present procedure, but an unavoidable issue in such transformation. Some pairs of r, phi do not exist, and therefore the method cannot infer these values automatically. Numpy assigns nan to these values and imshow exhibits these pixels in white. It is also important to notice that here it is important to limit the extent of \(r\) values, otherwise the corners will be included and artifacts introduced in the \(r\theta\) representation.

title(r'$I(r,\theta)$')
data_range = [[0,5], [-pi,pi]]
h1 = histogram2d(r.ravel(), phi.ravel(), bins=nbins, range=data_range, weights=(absolute(profile)**2).ravel())
h2 = histogram2d(r.ravel(), phi.ravel(), bins=nbins, range=data_range)

im = imshow(h1[0]/h2[0], origin='lower')
colorbar(im)

xlabel("$\\theta$")
ylabel("r")

# The present approach has errors close to r=0, since there will not be pixels with some values of theta
# Interpolation is necessary to fill out the gaps where h2[0]==0 close to r=0.
# The number of gaps reduces with the number of bins

savefig(r"assets\xy_rphi_transform.png")

We can also put the theoretically expected profile and the result of the numerical transformation side by side to see that the transformation is meaningful. Both patterns are very similar.

subplot(121)
title('Theoretical')
im = imshow(absolute(profile_r_phi)**2, origin='lower', cmap=im.cmap)
xlabel("$\\phi$")
ylabel("r")

subplot(122)
title('Transf. result')

imshow(h1[0]/h2[0], origin='lower', cmap=im.cmap)
xlabel("$\\phi$")
ylabel("r")

savefig(r"assets\xy_rphi_side_by_side.png")

The difference between both patterns above is also very small, as it can be seen from the image below.

title('Difference (Th-Tr)')
delta = absolute(absolute(profile_r_phi)**2 - h1[0]/h2[0])
im = imshow(delta, origin='lower')
colorbar(im)
xlabel("$\\phi$")
ylabel("r");
savefig(r"assets\xy_rphi_difference.png")